ЧиЗЪ:
- ХЗЦАРтЄЋЄщУЯЦАРтЄиЂЊЅГЅкЅыЅЫЅЏЅЙХЊХОВѓ
- ЄЗЄЋЄЗЁЂБпЕАЦЛЄђВОФъЄЙЄыЄШЁЂВаРБЄЮБПЦАЄђРтЬРЄЧЄЄЪЄЋЄУЄП
- ЁжДАСДЁзЄЧЄЂЄыЁжБпЁзЄђЧЫДўЄЗЁЂТЪБпЄШЄЗЄП
 :
:- ОЧХР
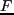 :
:- ФЙШОЗТ
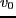 :
:- УЛШОЗТ
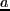
-
 : ЮЅПДЮЈ
: ЮЅПДЮЈ
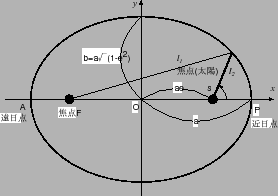
- ТЪБпЄЮУцПДЄЋЄщОЧХРЄоЄЧЄЮФЙЄЕ:
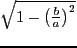
- ТЪБпЄЮЪ§ФјМАЁЇ
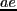
- БпЄЮЄШЄЁЂ
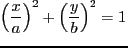
ДбТЌЅЧЁМЅПЄђВђРЯЄЗЄПЗыВЬЁЂЁжТРЭлЄШЯЧРБЄђЗыЄжРўЪЌЄЌАьФъЛўДжЄЫСнЄЏ ЬЬРбЄЯАьФъЄЧЄЂЄыЁзЄШЄЄЄІЗыЯРЄђЦРЄП
ЪЊЭ§ХЊЄЫЄЯЁЂГбБПЦАЮЬЪнТИТЇЄЫТаБўЁЃ
- ЅЈЅЭЅыЅЎЁМЪнТИТЇ
- БПЦАЮЬЪнТИТЇ
- БПЦАЅЈЅЭЅыЅЎЁМ
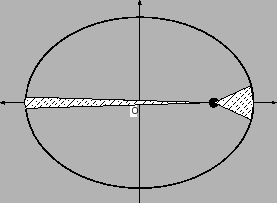
- БПЦАЮЬ
- ГбБПЦАЮЬ
(
![]()
![]() ЄЪЄщЁЂ
ЄЪЄщЁЂ
![]() .
.
ЄЄЄоЁЂ
ЄГЄГЄЧЬЬРбТЎХйЄЯ
 ЄЧЄЂЄыЁЃЄЙЄыЄШЁЂ
ЄЧЄЂЄыЁЃЄЙЄыЄШЁЂ
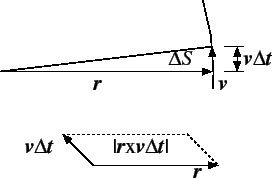
ДЪУБЄЮЄПЄсЁЂБпЕАЦЛЄђВОФъЄЙЄы
ЮЯЄЮЄФЄъЄЂЄЄ(ЫќЭАњЮЯ=БѓПДЮЯ)ЄшЄъЁЂ
ЄЂЄыЄЄЄЯЁЂБПЦАЪ§ФјМА(ЄПЄРЄЗ
ЄГЄьЄшЄъЁЂ
ЄЄЄоЁЂМўДќ
ЄЧЄЂЄыЄЋЄщЁЂ
ЄГЄьЄщЄшЄъЁЂ
ЄЄЄоЁЂУЯЕхЄЯ1ЧЏЄЧ1МўЄЗЁЂЕАЦЛШОЗТЄЯ1AUЄЪЄЮЄЧЁЂ
ЄШНёЄБЄыЁЃ