


Next: 密度揺らぎの統計的性質
Up: 密度揺らぎの成長則
Previous: 球対称解
領域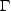 が collapse するとして、この領域の持つ角運動量がどうなるかを
調べよう[15,6,3,4,11]。角運動量
が collapse するとして、この領域の持つ角運動量がどうなるかを
調べよう[15,6,3,4,11]。角運動量 は、定義により
は、定義により
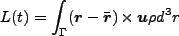 |
(3.104) |
ここで質量保存
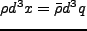 、
、
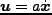 、
、
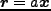 を使うと
を使うと
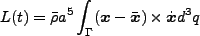 |
(3.105) |
となる。Zel'dovich 近似を用いると、
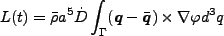 |
(3.106) |
である。ここで
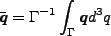 |
(3.107) |
である。これより領域の非球対称性が重要であることがわかる。
次に、potential 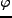 を
を
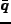 のまわりに展開する。
のまわりに展開する。
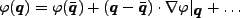 |
(3.108) |
これを式(3.78)に代入すると、
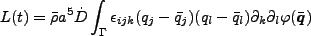 |
(3.109) |
となる。
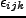 は完全反対称テンソルである。ここで potential の
微分の項を
は完全反対称テンソルである。ここで potential の
微分の項を
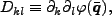 |
(3.110) |
inertial tensor を
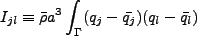 |
(3.111) |
とすると
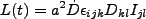 |
(3.112) |
となり、時間に依存する項を見ると、E-dS宇宙では
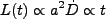 |
(3.113) |
と時間の一次に比例して増大することになる。実際には、maximum expansion の
あたりで角運動量の獲得は止まり、あとは保存して collapse することになる。
つまり
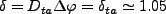 |
(3.114) |
となるところまで成長する。
inertia tensor を見ると、次元的に
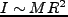 であり、上の式と合
わせて、これは
であり、上の式と合
わせて、これは
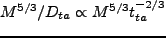 に比例する。こ
れより、maximum expansion での、即ち最終的にハローが獲得する角運動量は
に比例する。こ
れより、maximum expansion での、即ち最終的にハローが獲得する角運動量は
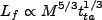 |
(3.115) |
となる。
通常、角運動量を議論する際は、無次元の spin parameter 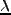 を用いる。
これは、
を用いる。
これは、
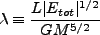 |
(3.116) |
で定義される。角運動量が0なら0、完全に rotation support になっていれば
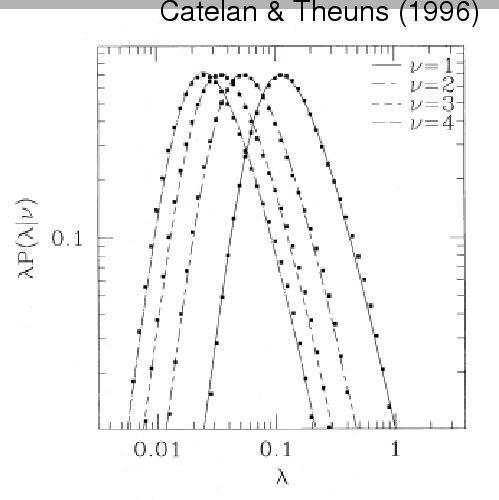
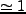 となる。図5に、Catelan & Theuns による
となる。図5に、Catelan & Theuns による
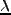 の分布を示す。詳細は略すが、これは初期に Gauss 分布する揺らぎの
場を考え、揺らぎのピークになる点のまわりの角運動量の分布がどうなるかを計
算したものである。パラメータになっている
の分布を示す。詳細は略すが、これは初期に Gauss 分布する揺らぎの
場を考え、揺らぎのピークになる点のまわりの角運動量の分布がどうなるかを計
算したものである。パラメータになっている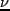 は揺らぎの高さの尺度で、揺
らぎの偏差を
は揺らぎの高さの尺度で、揺
らぎの偏差を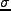 の何倍かを示す(
の何倍かを示す(
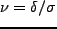 )。
)。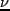 が大きいほ
ど早く collapse するので、それだけ獲得する角運動量も小さいということにな
る。
が大きいほ
ど早く collapse するので、それだけ獲得する角運動量も小さいということにな
る。
いづれの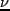 にしても、
にしても、
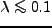 がほとんどを占めている。つまり、
ダークハローはほとんど回転していないということを示している。ただし、これ
が銀河になる際には内部のガスがエネルギーを失って収縮するため、結果的には
がほとんどを占めている。つまり、
ダークハローはほとんど回転していないということを示している。ただし、これ
が銀河になる際には内部のガスがエネルギーを失って収縮するため、結果的には
 となる。
となる。
この分布は、いわゆる log-normal分布で良く fit される。
![\begin{displaymath}
p(\lambda)d\lambda=
\frac{1}{\sqrt{2\pi}\sigma_{\lambda}}
\...
...n\bar{\lambda})^2}
{2\sigma_{\lambda}^{2}}\right] d\ln\lambda,
\end{displaymath}](img292.png) |
(3.117) |
ここで 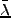 は平均の
は平均の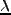 、
、
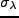 は
は 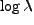 の分散である。大体
の分散である。大体
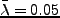 、
、
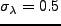 となる。
となる。
Figure 5:
 |



Next: 密度揺らぎの統計的性質
Up: 密度揺らぎの成長則
Previous: 球対称解
NAGASHIMA Masahiro
2009-03-12
![]() を
を
![]() のまわりに展開する。
のまわりに展開する。
![]() であり、上の式と合
わせて、これは
であり、上の式と合
わせて、これは
![]() に比例する。こ
れより、maximum expansion での、即ち最終的にハローが獲得する角運動量は
に比例する。こ
れより、maximum expansion での、即ち最終的にハローが獲得する角運動量は
![]() を用いる。
これは、
を用いる。
これは、
![]() にしても、
にしても、
![]() がほとんどを占めている。つまり、
ダークハローはほとんど回転していないということを示している。ただし、これ
が銀河になる際には内部のガスがエネルギーを失って収縮するため、結果的には
がほとんどを占めている。つまり、
ダークハローはほとんど回転していないということを示している。ただし、これ
が銀河になる際には内部のガスがエネルギーを失って収縮するため、結果的には
![]() となる。
となる。