


Next: 揺らぎの持つ角運動量の成長
Up: 密度揺らぎの成長則
Previous: 非線型領域
天体形成に至る非線型段階を記述するモデルとして、球対称に分布した揺らぎ
(質量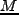 、半径
、半径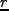 )に対する解がある。運動方程式は、単純に
)に対する解がある。運動方程式は、単純に
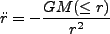 |
(3.92) |
であり、これがサイクロイド曲線
を描くことは良く知られている(ただし、宇宙項が存在すると斥力項がつく)。従っ
て、揺らぎの発展は、shell 内の平均密度が
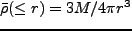 となることから求めることができる。初期(
となることから求めることができる。初期(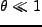 )の時、
)の時、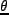 で展
開すると、
で展
開すると、
![\begin{displaymath}
\rho=\frac{3M}{4\pi r^{3}}=\frac{1}{6\pi Gt^{2}}\left[
1+\frac{3C}{20}\left(\frac{6t}{GM}\right)^{2/3}+\ldots\right]
\end{displaymath}](img241.png) |
(3.95) |
となる。いま、E-dS宇宙を考えると、平均密度は
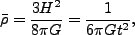 |
(3.96) |
線型揺らぎは
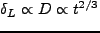 なので、上の球対称解は
なので、上の球対称解は
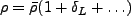 |
(3.97) |
とみなすことができる。
やがて、球殻内の自己重力により、球殻は宇宙膨張から切離されて収縮をはじめ
る。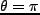 の時に
の時に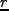 は最大になるが、これを maximum expansion、この
時期を turn around などと呼ぶ。この時の密度は、宇宙の平均密度に対して
は最大になるが、これを maximum expansion、この
時期を turn around などと呼ぶ。この時の密度は、宇宙の平均密度に対して
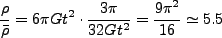 |
(3.98) |
であり、この時刻での線型揺らぎは
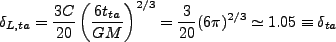 |
(3.99) |
となる。つまり、ある時刻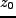 で揺らぎ
で揺らぎ
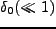 を持つ領域は、
線型揺らぎが
を持つ領域は、
線型揺らぎが
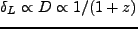 であることから、
であることから、
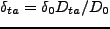 より
より
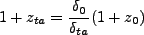 |
(3.100) |
となる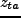 の時に最大膨張を迎えることになる。
の時に最大膨張を迎えることになる。
さらに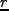 が再び0になる時点を collapse と定義すると(
が再び0になる時点を collapse と定義すると(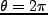 )、同様
にしてその時刻での線型揺らぎが
)、同様
にしてその時刻での線型揺らぎが
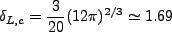 |
(3.101) |
となることがわかる。この時、実際の密度は形式的には発散するが、物理的に考
えると速やかに virial 平衡に達するであろう。この時の半径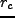 を求めよ
う。ここで、Energy保存を考慮し、turn around 時(速度0)と、collapse後
(virial平衡) を結ぶと、
を求めよ
う。ここで、Energy保存を考慮し、turn around 時(速度0)と、collapse後
(virial平衡) を結ぶと、
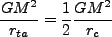 |
(3.102) |
となる。つまり、collapse 後の virial 半径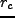 は、最大膨張時の半径
は、最大膨張時の半径
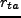 の半分であることがわかる。この時の平均密度に対する密度比は、
の半分であることがわかる。この時の平均密度に対する密度比は、
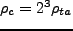 ,
, 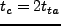 を考慮すると、
を考慮すると、
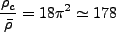 |
(3.103) |
となる。従って、collapse直後の天体の内部の平均密度は、その時刻での宇宙の
平均密度のおよそ200倍であることがわかる。
以上を用いると、揺らぎの amplitude を、現在まで線型成長を続けているとし
て normalize すると、ある点での揺らぎの大きさと、その点が collapse する
時刻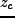 との間には、
との間には、
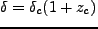 という関係のあ
ることがわかる(詳細は後述)。つまり、初期の揺らぎの分布を見れば、あ
る時刻でどれくらいの領域が collapse しているか、mapping することが可能に
なる。
という関係のあ
ることがわかる(詳細は後述)。つまり、初期の揺らぎの分布を見れば、あ
る時刻でどれくらいの領域が collapse しているか、mapping することが可能に
なる。



Next: 揺らぎの持つ角運動量の成長
Up: 密度揺らぎの成長則
Previous: 非線型領域
NAGASHIMA Masahiro
2009-03-12
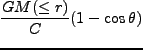
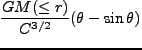
![]() の時に
の時に![]() は最大になるが、これを maximum expansion、この
時期を turn around などと呼ぶ。この時の密度は、宇宙の平均密度に対して
は最大になるが、これを maximum expansion、この
時期を turn around などと呼ぶ。この時の密度は、宇宙の平均密度に対して
![]() が再び0になる時点を collapse と定義すると(
が再び0になる時点を collapse と定義すると(![]() )、同様
にしてその時刻での線型揺らぎが
)、同様
にしてその時刻での線型揺らぎが
![]() との間には、
との間には、
![]() という関係のあ
ることがわかる(詳細は後述)。つまり、初期の揺らぎの分布を見れば、あ
る時刻でどれくらいの領域が collapse しているか、mapping することが可能に
なる。
という関係のあ
ることがわかる(詳細は後述)。つまり、初期の揺らぎの分布を見れば、あ
る時刻でどれくらいの領域が collapse しているか、mapping することが可能に
なる。