![]() -body simulation をやってみると、次の図のように線型と非線型の揺らぎが
対応がつくことが知られている(但し、図は個々の揺らぎではなく分散になって
いる)。
-body simulation をやってみると、次の図のように線型と非線型の揺らぎが
対応がつくことが知られている(但し、図は個々の揺らぎではなく分散になって
いる)。
一方、Lagrange座標での近似、即ち流体素片の運動を追いかける近似はかなり良
い結果を与えることが知られている。First order は Zel'dovich 近似として知
られ、流体素片の位置![]() は、その Lagrange 座標での位置
は、その Lagrange 座標での位置![]() と
と
| (3.84) |
| (3.85) |
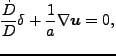 |
(3.86) | ||
| (3.87) | |||
| (3.88) |
なおこれは1次元シート重力系の exact解になっており、膨張宇宙では収縮する 領域の非等方性がますます強まるという性質を反映して良い近似になっていると 考えられる。
ただし、これもDM粒子のすり抜け(orbit crossing, shell crossing)が起こると 破綻する近似である。
ここで Zel'dovich 近似を用いた天体の崩壊を議論しておく。一様流体
(Lagrange座標
![]() )から崩壊するので、質量保存より
)から崩壊するので、質量保存より
| (3.89) |
| (3.90) |
| (3.91) |