


Next: 密度揺らぎの smoothing
Up: 密度揺らぎの統計的性質
Previous: 密度揺らぎの統計的性質
密度揺らぎ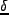 は、
は、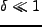 の時代には通常 random Gaussian 揺らぎ
であると仮定される。揺らぎの分散を
の時代には通常 random Gaussian 揺らぎ
であると仮定される。揺らぎの分散を
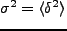 と置
くと、一点分布関数は
と置
くと、一点分布関数は
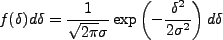 |
(4.118) |
となる。ここで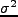 は揺らぎの分散であり、
は揺らぎの分散であり、
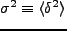 である。
である。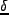 のFourier変換は、
のFourier変換は、
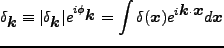 |
|
|
(4.119) |
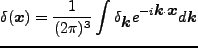 |
|
|
(4.120) |
であり、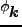 は
は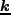 成分の位相である。random Gaussian 揺らぎ
は位相に相関がなく、
成分の位相である。random Gaussian 揺らぎ
は位相に相関がなく、
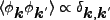 |
(4.121) |
である。amplitude の自乗平均は、power spectrum と呼ばれ、
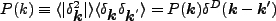 |
(4.122) |
で定義される。ここで
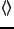 は ensemble平均を表し、また一様等方
性より
は ensemble平均を表し、また一様等方
性より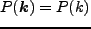 とした。重要な関係として、二体相関関数
とした。重要な関係として、二体相関関数
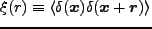 と
と
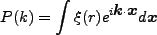 |
(4.123) |
というFourier変換の関係にある。また、Gaussian random field の特徴として、
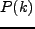 或いは
或いは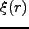 によって、一意的に分布が定まる。
によって、一意的に分布が定まる。
次に、power spectrum の時間進化を見よう。通常、inflation直後に生成される
揺らぎは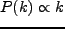 と仮定され、Harrison-Zel'dovich spectrum と呼ばれ
る。
と仮定され、Harrison-Zel'dovich spectrum と呼ばれ
る。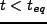 では horizon より大きい揺らぎは
では horizon より大きい揺らぎは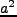 に比例して成長し、
horizon 内の揺らぎは成長しない。一方、
に比例して成長し、
horizon 内の揺らぎは成長しない。一方、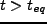 の揺らぎは、どのスケー
ルでも一様に成長する。従って、その様子を図に描くと、FIG.6
のようになる。なお、分散に直すと、
の揺らぎは、どのスケー
ルでも一様に成長する。従って、その様子を図に描くと、FIG.6
のようになる。なお、分散に直すと、
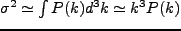 であるから、短波長側(
であるから、短波長側(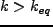 )では
)では
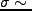 となる。ただし、実際には完全に成長が止まるわけ
ではなく、
となる。ただし、実際には完全に成長が止まるわけ
ではなく、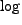 的な成長があるため、完全に一定値になるわけではない。
的な成長があるため、完全に一定値になるわけではない。
Figure 6:
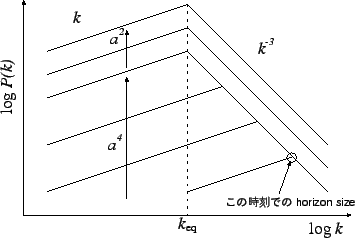 |
Figure 7:
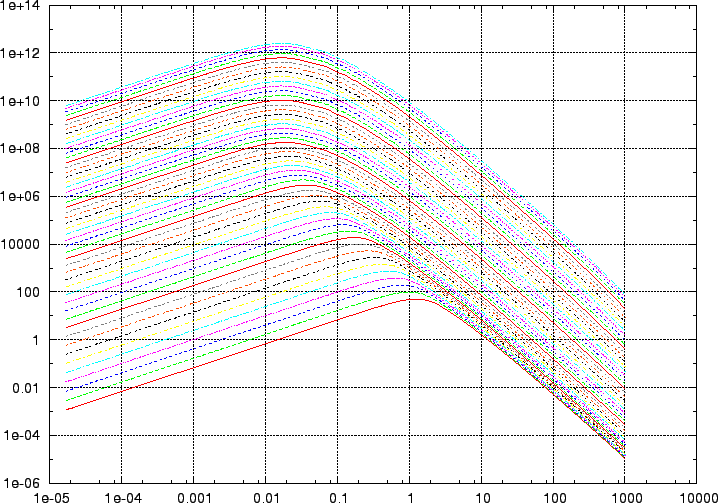 |
詳細な計算では、power spectrum を initial (Harrison-Zel'dovich)とそこか
らの変形(transfer function)に分けて、
![\begin{displaymath}
T(k)=\frac{\ln(1+2.34q)}{2.34q}\left[
1+3.89q+(16.1q)^{2}+(5.46q)^{3}+(6.71q)^{4}\right]^{-1/4},
\end{displaymath}](img324.png) |
(4.124) |
ここで
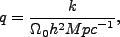 |
(4.125) |
得られる power spectrum は
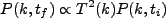 |
(4.126) |
となる。ここで
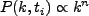 |
(4.127) |
であり、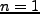 なら Harrison-Zel'dovich spectrum である。
なら Harrison-Zel'dovich spectrum である。



Next: 密度揺らぎの smoothing
Up: 密度揺らぎの統計的性質
Previous: 密度揺らぎの統計的性質
NAGASHIMA Masahiro
2009-03-12
![]() と仮定され、Harrison-Zel'dovich spectrum と呼ばれ
る。
と仮定され、Harrison-Zel'dovich spectrum と呼ばれ
る。![]() では horizon より大きい揺らぎは
では horizon より大きい揺らぎは![]() に比例して成長し、
horizon 内の揺らぎは成長しない。一方、
に比例して成長し、
horizon 内の揺らぎは成長しない。一方、![]() の揺らぎは、どのスケー
ルでも一様に成長する。従って、その様子を図に描くと、FIG.6
のようになる。なお、分散に直すと、
の揺らぎは、どのスケー
ルでも一様に成長する。従って、その様子を図に描くと、FIG.6
のようになる。なお、分散に直すと、
![]() であるから、短波長側(
であるから、短波長側(![]() )では
)では
![]() となる。ただし、実際には完全に成長が止まるわけ
ではなく、
となる。ただし、実際には完全に成長が止まるわけ
ではなく、![]() 的な成長があるため、完全に一定値になるわけではない。
的な成長があるため、完全に一定値になるわけではない。