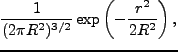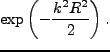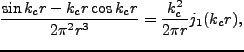Next: 二体相関関数
Up: 密度揺らぎの統計的性質
Previous: Gauss分布
通常仮定されるCDMのpower spectrumは紫外発散を起こしているので、意味のあ
る揺らぎにするために粗視化(smoothing)を実行する。以下では、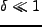 の状況のみ考えるが、前章の議論から、線型段階の
の状況のみ考えるが、前章の議論から、線型段階の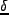 と非線型の
と非線型の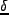 は球対称解を用いて mapping できるので、球対称解の範囲で非線型成長も考慮
できることになる。
は球対称解を用いて mapping できるので、球対称解の範囲で非線型成長も考慮
できることになる。
適切なWindow関数
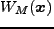 を考える。これは、空間積分を実行すると1になるよ
うに規格化されているものである。また、以降の議論では、球対称なものを考え
る。添字の
を考える。これは、空間積分を実行すると1になるよ
うに規格化されているものである。また、以降の議論では、球対称なものを考え
る。添字の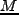 は、smoothing scale
は、smoothing scale 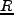 が球対称で質量が
が球対称で質量が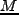 の領域に相当すること
を意味し、
の領域に相当すること
を意味し、
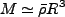 |
(4.128) |
となる。この時、scale 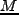 の密度揺らぎ場は、
の密度揺らぎ場は、
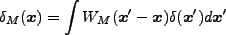 |
(4.129) |
で表される。
一方、揺らぎをFourier成分で表すと便利であったので、Window関数もFourier変
換しておくと、
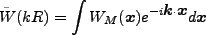 |
(4.130) |
となる。ここで、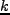 空間での cut-off scale を
空間での cut-off scale を 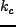 とおくと、
とおくと、
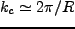 である。これを用いると、
である。これを用いると、
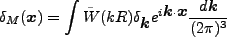 |
(4.131) |
となる。この粗視化された場で、
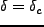 となる点が、粗視化のスケー
ルで天体として collapse すると考えることができる。
となる点が、粗視化のスケー
ルで天体として collapse すると考えることができる。
以下に、しばしば用いられるWindow関数(filter)の形を挙げておく。
- Top-hat filter
- Gaussian filter
- Sharp
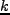 -space filter
-space filter
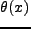 は Heaviside の step function である。
は Heaviside の step function である。



Next: 二体相関関数
Up: 密度揺らぎの統計的性質
Previous: Gauss分布
NAGASHIMA Masahiro
2009-03-12
![]() を考える。これは、空間積分を実行すると1になるよ
うに規格化されているものである。また、以降の議論では、球対称なものを考え
る。添字の
を考える。これは、空間積分を実行すると1になるよ
うに規格化されているものである。また、以降の議論では、球対称なものを考え
る。添字の![]() は、smoothing scale
は、smoothing scale ![]() が球対称で質量が
が球対称で質量が![]() の領域に相当すること
を意味し、
の領域に相当すること
を意味し、