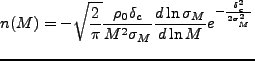

Next: より現実的な質量関数
Up: 密度揺らぎの統計的性質
Previous: 二体相関関数
ここでは球対称解と揺らぎの Gaussian 分布から、質量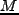 の天体の個数密度
の天体の個数密度
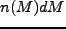 を見積る Press-Schechter 近似を紹介する[14]。
を見積る Press-Schechter 近似を紹介する[14]。
さて、smoothing scale 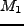 で
で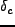 を越える質量(領域)は、
を越える質量(領域)は、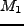 より
も大きい天体として collapse するはずである。なぜならば、
より
も大きい天体として collapse するはずである。なぜならば、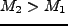 となる
より大きいスケールで smoothing を行えば、丁度
となる
より大きいスケールで smoothing を行えば、丁度
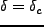 となるスケー
ルが存在するはずだからである。従って、スケール
となるスケー
ルが存在するはずだからである。従って、スケール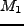 の場で
の場で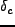 を越
える領域は、質量
を越
える領域は、質量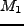 より大きい天体として collapse する領域内にある、
より大きい天体として collapse する領域内にある、
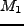 で smoothing した時に
で smoothing した時に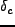 を越える領域の和に等しい。
この「
を越える領域の和に等しい。
この「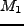 でsmoothingした時に
でsmoothingした時に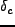 を越える確率(あるいは全宇宙にお
いて
を越える確率(あるいは全宇宙にお
いて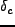 を越える領域にある質量の割合)」を
を越える領域にある質量の割合)」を
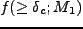 と置
くと、解くべき方程式は
と置
くと、解くべき方程式は
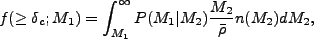 |
(4.143) |
となる。ここで、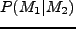 は、
は、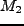 field で丁度
field で丁度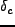 となる点で、
となる点で、
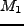 field では
field では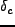 を越える確率、
を越える確率、
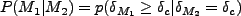 |
(4.144) |
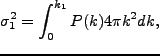
である。これを求めるためには、条件付き確率を求めなければならない。そして、
条件付き確率を求めるためには、2変数(
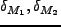 )のGauss
分布を考える必要がある。
)のGauss
分布を考える必要がある。
一般に、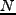 変数のGauss分布は次のように書ける:
変数のGauss分布は次のように書ける:
![\begin{displaymath}
p({\bf V}^{N})d{\bf V}^{N}=\frac{\exp[-Q/2]}{\sqrt{(2\pi)^{N}\det({\bf M})}}d{\bf V}^{N},
\end{displaymath}](img382.png) |
(4.145) |
ここで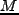 は covariance matrix であり、また
は covariance matrix であり、また
である。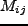 の要素を sharp
の要素を sharp 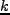 -space filter の場合に具体的に考えると、
-space filter の場合に具体的に考えると、
である。いまは filter の性質により、covariance が 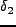 の分散と同じ
になることに注意。逆行列は
の分散と同じ
になることに注意。逆行列は
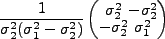 |
(4.151) |
となるので、
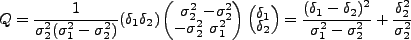 |
(4.152) |
となる。これより、
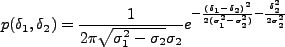 |
(4.153) |
となることがわかるが、
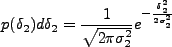 |
(4.154) |
であることに注意すると、
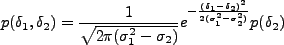 |
(4.155) |
であるから、条件付き確率は
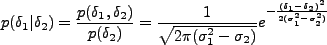 |
(4.156) |
となる。つまり、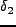 が指定されている場合、そこからのズレは、
smoothing scale の違いがもたらす分散のズレを分散とする Gaussian になるこ
とがわかる。
が指定されている場合、そこからのズレは、
smoothing scale の違いがもたらす分散のズレを分散とする Gaussian になるこ
とがわかる。
これを用いると、
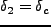 の時に、
の時に、
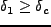 となる
確率は、
となる
確率は、
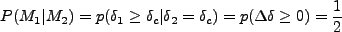 |
(4.157) |
となる。
これを元の積分方程式に入れると、
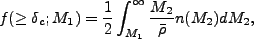 |
(4.158) |
となる。
さて、これを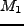 で微分してみよう。すると、
で微分してみよう。すると、
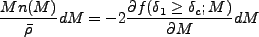 |
(4.159) |
となる。ここで、変数を正規化してやると、
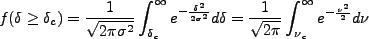 |
(4.160) |
ここで
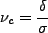 |
(4.161) |
である。従って、
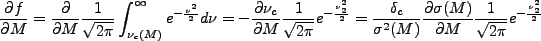 |
(4.162) |
以上より、
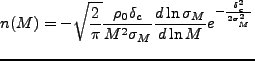 |
|
|
(4.163) |
となる。これをPress-Schechter質量関数と呼ぶが、 の場合のみ適用可能
であることに注意しなければならない。small mass scale では、
の場合のみ適用可能
であることに注意しなければならない。small mass scale では、
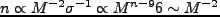 となる。
となる。


Next: より現実的な質量関数
Up: 密度揺らぎの統計的性質
Previous: 二体相関関数
NAGASHIMA Masahiro
2009-03-12
![]() で
で![]() を越える質量(領域)は、
を越える質量(領域)は、![]() より
も大きい天体として collapse するはずである。なぜならば、
より
も大きい天体として collapse するはずである。なぜならば、![]() となる
より大きいスケールで smoothing を行えば、丁度
となる
より大きいスケールで smoothing を行えば、丁度
![]() となるスケー
ルが存在するはずだからである。従って、スケール
となるスケー
ルが存在するはずだからである。従って、スケール![]() の場で
の場で![]() を越
える領域は、質量
を越
える領域は、質量![]() より大きい天体として collapse する領域内にある、
より大きい天体として collapse する領域内にある、
![]() で smoothing した時に
で smoothing した時に![]() を越える領域の和に等しい。
この「
を越える領域の和に等しい。
この「![]() でsmoothingした時に
でsmoothingした時に![]() を越える確率(あるいは全宇宙にお
いて
を越える確率(あるいは全宇宙にお
いて![]() を越える領域にある質量の割合)」を
を越える領域にある質量の割合)」を
![]() と置
くと、解くべき方程式は
と置
くと、解くべき方程式は
![]() 変数のGauss分布は次のように書ける:
変数のGauss分布は次のように書ける:
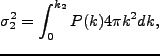
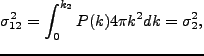
![]() の時に、
の時に、
![]() となる
確率は、
となる
確率は、
![]() で微分してみよう。すると、
で微分してみよう。すると、