さて、幾何学を決めるためには距離を定義しなければならない。良く知られてい
る重要な距離として、角径距離(angular-diameter distance)と光度距離
(luminosity distance)がある。角径距離
![]() は天体の大きさDと見込
む角度
は天体の大きさDと見込
む角度![]() から与えられる距離で、
から与えられる距離で、
![]() で与えら
れ、赤方偏移と
で与えら
れ、赤方偏移と
![]() の関係にある。一方、光度距離
の関係にある。一方、光度距離![]() は、天体の光度Lと観測されるflux fから
は、天体の光度Lと観測されるflux fから
![]() で定義される。これは
で定義される。これは
![]() という関係になり、
という関係になり、![]() では
角径距離と一致するが、遠方では振舞いが異なってくる。なお、rは、良く知
られているように、
では
角径距離と一致するが、遠方では振舞いが異なってくる。なお、rは、良く知
られているように、
![]() を通じて、
を通じて、
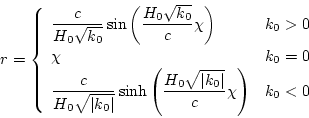 |
(14) |
さて、今大きさが既知の天体があるとしよう。よく用いられるのは、電波銀河の
core radius Dである。赤方偏移zにある電波銀河の core が、見込む角
![]() で観測された場合、角径距離を用いて
で観測された場合、角径距離を用いて
![]() となり、rを決められる。
となり、rを決められる。
次に、光度が既知の天体を考える。例えば、Ia型超新星の光度曲線から光度を求
めることができる。ある波長領域での光度![]() と観測される flux
と観測される flux
![]() とは
とは
![]() の関係にあるので、超新
星の赤方偏移を観測すればrが決まる。
の関係にあるので、超新
星の赤方偏移を観測すればrが決まる。
また、
![]() と
と![]() を組合せる方法もある。銀河の光度分布を仮
定すると、単位視野の中での銀河の等級ごとの個数を求めることができる。観測
的には、ある方向を深く見て、写った銀河の数を数えればよい。銀河計数
(galaxy number counts)とか個数-等級関係(number-magnitude relation)などと
呼ばれる。
を組合せる方法もある。銀河の光度分布を仮
定すると、単位視野の中での銀河の等級ごとの個数を求めることができる。観測
的には、ある方向を深く見て、写った銀河の数を数えればよい。銀河計数
(galaxy number counts)とか個数-等級関係(number-magnitude relation)などと
呼ばれる。
これら幾何学的テストには幾つかの問題点がある。それは、宇宙論パラメータと
時空の幾何学自体は密接に関係しているが、その幾何学を測る probe となる天
体に対し、何らかの仮定(あるいはモデル)をおかざるを得ないことである。また、
宇宙論パラメータによる違いは十分遠方(
![]() )でないと現れてこない。従っ
て、それだけ観測的にも難しくなる。さらに、それだけ遠方になると、天体の進
化効果も無視できなくなることが多い。例えば、現在の典型的な銀河と、z>1での銀河は異なった特徴を示すと考えられている。そこで、幾何学的テストを用
いて信頼できる結果を得るには、probe となる天体について物理的に明確な知識
を得ることが必須となる。つまり、その天体自身についてより詳細な研究が必要
である、ということである。
)でないと現れてこない。従っ
て、それだけ観測的にも難しくなる。さらに、それだけ遠方になると、天体の進
化効果も無視できなくなることが多い。例えば、現在の典型的な銀河と、z>1での銀河は異なった特徴を示すと考えられている。そこで、幾何学的テストを用
いて信頼できる結果を得るには、probe となる天体について物理的に明確な知識
を得ることが必須となる。つまり、その天体自身についてより詳細な研究が必要
である、ということである。