

Next: 幾何学的テスト
Up: Hubble parameter H
Previous: 重力レンズ像間の時間変動の差
宇宙には 3K のCMB photon が充満しているが、これが銀河団内の高温の電離ガ
ス(
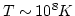 )と衝突すると、逆compton散乱により、エネルギーを与えられ
る。これは CMB の Rayleigh-Jeans 側の photon を減らし、Wien 側に運ぶので、
低温側ではより低温に、高温側ではより高温になったように見える。銀河団のサ
イズをlcとし、球対称であると仮定すると、CMB の温度変化から奥行きを推
定できるので、銀河団の実直径がわかることになる。従って、それを銀河団を見
込む角度
)と衝突すると、逆compton散乱により、エネルギーを与えられ
る。これは CMB の Rayleigh-Jeans 側の photon を減らし、Wien 側に運ぶので、
低温側ではより低温に、高温側ではより高温になったように見える。銀河団のサ
イズをlcとし、球対称であると仮定すると、CMB の温度変化から奥行きを推
定できるので、銀河団の実直径がわかることになる。従って、それを銀河団を見
込む角度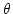 と比較することによって、H0を得ることができる。
と比較することによって、H0を得ることができる。
銀河団ガス(ICM)のX線表面輝度SXは、
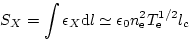 |
(11) |
で与えられる。ここで
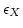 はemissivity、
はemissivity、
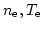 はICM
の電子密度及び温度である。一方、CMBの温度変化
はICM
の電子密度及び温度である。一方、CMBの温度変化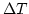 は
は
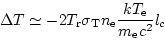 |
(12) |
と書ける。ここで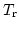 はCMBの温度、
はCMBの温度、
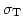 はThomson断面積
である。ここから密度を消去すると、
はThomson断面積
である。ここから密度を消去すると、
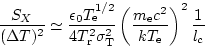 |
(13) |
となり、
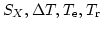 を観測してlcを求めること
ができる。あとは
を観測してlcを求めること
ができる。あとは
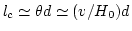 であるから、銀河団の視
直径と赤方偏移からH0が求まる。この方法では、例えば
であるから、銀河団の視
直径と赤方偏移からH0が求まる。この方法では、例えば
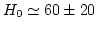 km s-1 Mpc-1という値が得られている[7]。
km s-1 Mpc-1という値が得られている[7]。
NAGASHIMA Masahiro
2000-10-23