

Next: Sunyaev-Zel'dovich 効果
Up: Hubble parameter H
Previous: 膨張率の直接測定
強い重力レンズは複数の像を生む。ソース天体が時間変動していると、像間の光
路差により、各像の変動には時間差が生じる。この時間差と、像間の角度差、赤
方偏移から、以下のようにしてH0を求めることができる。
Figure 2:
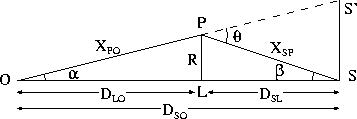 |
FIG.2に従って、質量MのレンズLによる曲がり角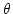 は
(point mass と仮定)、
は
(point mass と仮定)、
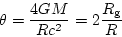 |
(9) |
と書ける。ここで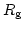 はSchwartzschild 半径である。
はSchwartzschild 半径である。
 と近似すると、光路差
と近似すると、光路差
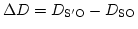 は
は
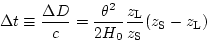 |
(10) |
と書けることがわかる。ここで、
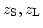 はそれぞれソース天体、
レンズの赤方偏移であり、観測可能量である。従って、あとは像の位置
はそれぞれソース天体、
レンズの赤方偏移であり、観測可能量である。従って、あとは像の位置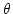 を観測し、像の時間変動をモニターして時間差
を観測し、像の時間変動をモニターして時間差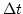 を求めれば、H0が
わかる。幸いにして、時間差は年のオーダーである。この方法を用いて
を求めれば、H0が
わかる。幸いにして、時間差は年のオーダーである。この方法を用いて
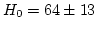 km s-1 Mpc-1という値が報告されている[6]。
km s-1 Mpc-1という値が報告されている[6]。
NAGASHIMA Masahiro
2000-10-23

![]() は
(point mass と仮定)、
は
(point mass と仮定)、