高密度領域
→原子同士が衝突しやすい
→分子(COなど)ができやすい⇒分子雲
分子雲内の密度の高いところ→分子雲コア…星の「種」
◎重力不安定…自己重力でガス雲は収縮できるか?

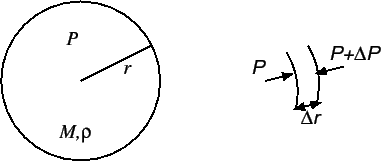
◎簡単な評価
圧力勾配を
 と簡単に近似する
と簡単に近似する
ここで音速
![]()
収縮する時間スケール(free-fall time)
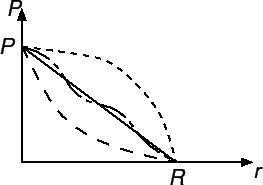
★典型的なスケール
◎収縮をはじめるとどうなるか?→熱力学
熱力学第一法則(エネルギー保存則)
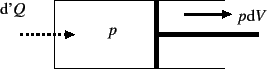
| |
注入されたエネルギー(熱量) | |
| |
内部エネルギー | |
| |
仕事 |
| |
モル数 |
| |
定積比熱。1mol当たり、1K上昇させるのに必要な熱量 |
| |
定圧比熱。 |
![]() >1=1<1
>1=1<1
| のとき、 | ↓で | ↓ | 収縮しない |
| のとき、 | ↓で | ↑ | 収縮する |
| 単原子分子気体 | → | |
| 二原子分子気体 | → |
→ほぼ等温で収縮、
、収縮できる
→星が作られる