


Next: 線型領域
Up: 密度揺らぎの成長則
Previous: 膨張宇宙での流体方程式
次に、摂動論を考えよう。まずはゼロ次を考える。速度については、固有速度
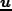 自体が摂動であることに注意する。
自体が摂動であることに注意する。
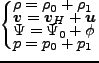 |
|
|
(3.63) |
これらより、ゼロ次の方程式は
となる。
まず連続の式を見てみよう。これは以下のように容易に変形できる。
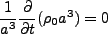 |
(3.67) |
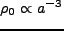 であるから、これは質量保存の法則、あるいは断熱膨張を示している。
であるから、これは質量保存の法則、あるいは断熱膨張を示している。
次に運動方程式であるが、両辺に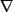 を作用させると、
を作用させると、
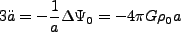 |
(3.68) |
となり、結局
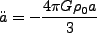 |
(3.69) |
となり、Friedmann方程式に一致する。
NAGASHIMA Masahiro
2009-03-12
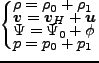
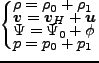
![]() を作用させると、
を作用させると、