


Next: バックグラウンド
Up: 密度揺らぎの成長則
Previous: 運動方程式
次に、background が膨張しているもとでの流体力学方程式を考える。
既に述べたように、空間座標は物理的な距離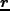 と共動座標
と共動座標
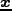 の両方で表され、
これらの関係はscale factorを通じて
の両方で表され、
これらの関係はscale factorを通じて
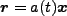 |
(3.53) |
となっている。前節で導いた流体力学方程式は当然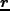 についてのものであるた
め、ここでは
についてのものであるた
め、ここでは
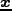 についての式に書き直し、宇宙膨張の効果がどのように表れる
かを見てみよう。
についての式に書き直し、宇宙膨張の効果がどのように表れる
かを見てみよう。
まず空間微分については、上の関係より
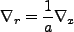 |
(3.54) |
となる(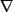 の添字はどの座標での微分を実行するかを示す)。次に時間微分
であるが、まず上の関係式より速度は
の添字はどの座標での微分を実行するかを示す)。次に時間微分
であるが、まず上の関係式より速度は
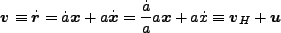 |
(3.55) |
と書ける。ここで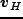 は宇宙膨張の速度であり、
は宇宙膨張の速度であり、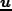 はそこからのズレ(固有
速度)である。
はそこからのズレ(固有
速度)である。
これらを用いると、Lagrange微分の特性から、
となることがわかる。若干変形すると、
となる(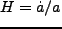 )。従って、
)。従って、
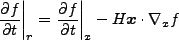 |
(3.59) |
である。無論、式(3.15)のように導いても同じことである。
以上をふまえて、Euler形式での膨張宇宙における流体力学方程式を書くと(添字
のない偏微分は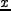 での微分)、
での微分)、
となる。



Next: バックグラウンド
Up: 密度揺らぎの成長則
Previous: 運動方程式
NAGASHIMA Masahiro
2009-03-12
![]() と共動座標
と共動座標
![]() の両方で表され、
これらの関係はscale factorを通じて
の両方で表され、
これらの関係はscale factorを通じて
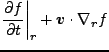
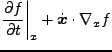
![$\displaystyle \left.\frac{\partial
f}{\partial t}\right\vert _x-\left(
\v\cdot\...
...artial t}\right\vert _x-
\left([\v _H+\u ]\cdot\nabla_r-\u\cdot\nabla_r\right)f$](img140.png)
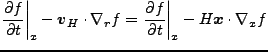
![]() での微分)、
での微分)、