


Next: 膨張宇宙での流体方程式
Up: 流体近似
Previous: 連続の式
次に、体積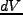 の流体素片についての運動方程式を考えよう。
の流体素片についての運動方程式を考えよう。
Newtonの運動方程式より、力を
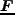 とすると、
とすると、
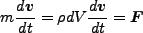 |
(3.46) |
となる(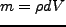 )。次に力を考える。一つは重力であり、重力ポテンシャル
を
)。次に力を考える。一つは重力であり、重力ポテンシャル
を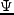 とおくと、力は
とおくと、力は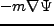 である。重力ポテンシャルと密度との関
係は、
である。重力ポテンシャルと密度との関
係は、
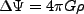 |
(3.47) |
である(Poisson方程式)。
次に流体の場合も考慮して圧力に起因する力を考えておく。ここでも簡単のため
にまずは一次元系で考えよう。流体素片の断面積をSとおき、奥行を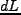 とする
と(
とする
と(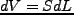 )、圧力勾配による力は
)、圧力勾配による力は
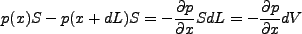 |
(3.48) |
三次元の場合は方向ベクトルを掛けて足し上げれば良いので、単純に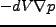 となる。
となる。
まとめると、運動方程式は
となる。これをEuler方程式と呼ぶ。もし粘性などを考慮すると、右辺の力の項
にそれらが加わることになる(Navier-Stokes方程式)。
以上より、解くべき式は、Lagrange形式で書くと
である。
NAGASHIMA Masahiro
2009-03-12
![]() とすると、
とすると、
![]() とする
と(
とする
と(![]() )、圧力勾配による力は
)、圧力勾配による力は