

Next: 運動方程式
Up: 流体近似
Previous: 流体近似
まず、連続の式(質量保存の式)をLagrange的に考える。体積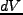 の流体素片の
質量は
の流体素片の
質量は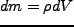 であるが、これが保存するので
であるが、これが保存するので
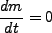 |
(3.29) |
である。分解すると、
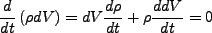 |
(3.30) |
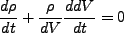 |
(3.31) |
となる。ここで簡単のため左右にのびた一次元系を考えると、第二項は流体素片の体積の時間
変化であり、それはこの流体素片の右側の端の速度-左側の端の速度、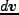 で与えられ
る。即ち、
で与えられ
る。即ち、
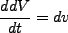 |
(3.32) |
これを用いると、
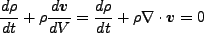 |
(3.33) |
となる。
次にEuler的に見てみよう。
一辺が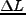 の固定された微小な立方体を考える(
の固定された微小な立方体を考える(
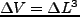 、
、
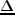 は空間的に固定された微小量を示すものとする)。この立方体内
の物質の増減を調べよう。この立方体の質量の増減は、立方体への流入・流出に
よるので(湧き出し・吸い込みはない)、質量の変化
は空間的に固定された微小量を示すものとする)。この立方体内
の物質の増減を調べよう。この立方体の質量の増減は、立方体への流入・流出に
よるので(湧き出し・吸い込みはない)、質量の変化
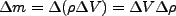 |
(3.34) |
がゼロでないとすると、必然的に流れがあることになる。ここで体積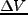 は一定であることを使った。
は一定であることを使った。
次に、流れがあるとき、この立方体に流れ込む・流れ出す物質の量を求めよう。
簡単のため、流れの方向は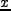 軸方向であるとする。
速度
軸方向であるとする。
速度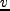 で物質が流れているとき、時間
で物質が流れているとき、時間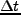 の間に入ってくる物質の
量、出ていく物質の量の差は、
の間に入ってくる物質の
量、出ていく物質の量の差は、
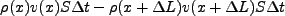 |
(3.35) |
となる。ここで立方体の面積
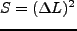 である。ここで質量流束
である。ここで質量流束
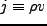 を定義すると、上式は
を定義すると、上式は
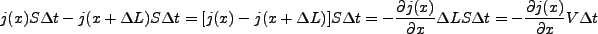 |
(3.36) |
と変形できる。ここで Taylor 展開を使った。
さて、式(3.6)、(3.8)は等しいはずであるから、
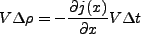 |
(3.37) |
である。両辺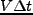 で割ると、
で割ると、
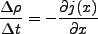 |
(3.38) |
となるが、左辺は空間を固定し、時間だけを変化させた場合の質量の変化に相当
するので、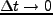 の極限では、これは時間の偏微分を意味する。従っ
て、
の極限では、これは時間の偏微分を意味する。従っ
て、
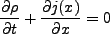 |
(3.39) |
となる。
いままでは、流れは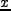 方向だけと仮定していたが、一般化するとベクトルで書
くことができ、
方向だけと仮定していたが、一般化するとベクトルで書
くことができ、
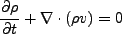 |
(3.40) |
と書ける。ここで
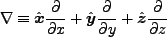 |
(3.41) |
である。
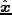 などは単位ベクトルである。
などは単位ベクトルである。
さて、Lagrange形式とEuler形式のそれぞれを見比べてみると、Lagrange微分は
以下の関係があることがわかる。
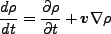 |
(3.42) |
本当にこれが成り立っているかを考えよう。簡単のために、また一次元系で考え
る。Lagrange微分の中身を考えてみると、
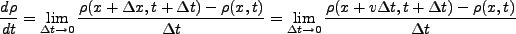 |
(3.43) |
ここで
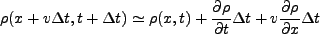 |
(3.44) |
であるので、結局
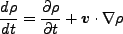 |
(3.45) |
となり、実際に成り立っていることがわかる。

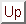

Next: 運動方程式
Up: 流体近似
Previous: 流体近似
NAGASHIMA Masahiro
2009-03-12
![]() の固定された微小な立方体を考える(
の固定された微小な立方体を考える(
![]() 、
、
![]() は空間的に固定された微小量を示すものとする)。この立方体内
の物質の増減を調べよう。この立方体の質量の増減は、立方体への流入・流出に
よるので(湧き出し・吸い込みはない)、質量の変化
は空間的に固定された微小量を示すものとする)。この立方体内
の物質の増減を調べよう。この立方体の質量の増減は、立方体への流入・流出に
よるので(湧き出し・吸い込みはない)、質量の変化
![]() 軸方向であるとする。
速度
軸方向であるとする。
速度![]() で物質が流れているとき、時間
で物質が流れているとき、時間![]() の間に入ってくる物質の
量、出ていく物質の量の差は、
の間に入ってくる物質の
量、出ていく物質の量の差は、
![]() 方向だけと仮定していたが、一般化するとベクトルで書
くことができ、
方向だけと仮定していたが、一般化するとベクトルで書
くことができ、