


Next: 連続の式
Up: 密度揺らぎの成長則
Previous: 密度揺らぎの成長則
ここでは、考えている領域の大きさが horizon より十分小さい、物質の速度が
光速に比べ十分小さい、という Newton 近似、及び考えている領域の大きさが、
考えている物質の平均自由行程より十分大きい、という流体近似が成り立つ場合
を考える。銀河や銀河団スケールでは、CDMモデルで recombination 以降を考え
る限り、以上の仮定は十分成り立つと考えてよい。
流体近似が使えるのは微小な密度揺らぎが自己重力でジワジワと集まって
くるような場合のみであり、ひとたび collapse してしまうとDM粒子の速度が空
間の一価関数ではなくなるため近似が破綻する。このような場合には、原理的に
は Boltzmann 方程式に戻って考えなければならない。
ダークマターは相互作用の弱い物質であるため、無衝突粒子として扱うことにな
る。このような場合、本来はBoltzmann方程式を解く必要があるが、これは自由度
が大きすぎ解くのが困難である。ところが、いま考えているのはCDMである。CDM
は定義により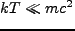 であるため、速度分散は非常に小さい。すると、空間
のある点における粒子の速度はほぼ揃っており、速度場
であるため、速度分散は非常に小さい。すると、空間
のある点における粒子の速度はほぼ揃っており、速度場
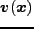 として考えれば
良いことになる。すると、ダークマターの運動は圧力ゼロ、粘性なしの流体力学
方程式に従うことになる。
として考えれば
良いことになる。すると、ダークマターの運動は圧力ゼロ、粘性なしの流体力学
方程式に従うことになる。
以下では、硬い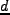 がLagrange微分を示すものとする。流体力学方程式の導出に
ついてはAppendixを参照のこと。
がLagrange微分を示すものとする。流体力学方程式の導出に
ついてはAppendixを参照のこと。
Subsections
NAGASHIMA Masahiro
2009-03-12
![]() であるため、速度分散は非常に小さい。すると、空間
のある点における粒子の速度はほぼ揃っており、速度場
であるため、速度分散は非常に小さい。すると、空間
のある点における粒子の速度はほぼ揃っており、速度場
![]() として考えれば
良いことになる。すると、ダークマターの運動は圧力ゼロ、粘性なしの流体力学
方程式に従うことになる。
として考えれば
良いことになる。すると、ダークマターの運動は圧力ゼロ、粘性なしの流体力学
方程式に従うことになる。
![]() がLagrange微分を示すものとする。流体力学方程式の導出に
ついてはAppendixを参照のこと。
がLagrange微分を示すものとする。流体力学方程式の導出に
ついてはAppendixを参照のこと。