


Next: Friedmann方程式の意味
Up: note
Previous: はじめに
通常、宇宙は一様・等方と仮定される(宇宙原理)。いま、宇宙項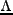 を含む Einstein方程式
を含む Einstein方程式
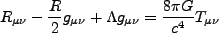 |
(2.1) |
を考える。ここで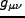 はメトリック、
はメトリック、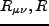 はそれぞれリッ
チテンソル及びリッチスカラー、
はそれぞれリッ
チテンソル及びリッチスカラー、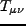 はエネルギー運動量テンソルであ
る。ここで一様等方を示す Robertson-Walker metric
はエネルギー運動量テンソルであ
る。ここで一様等方を示す Robertson-Walker metric
![\begin{displaymath}
ds^{2}=-c^{2}dt^{2}+a^{2}(t)\left[\frac{dx^{2}}{\sqrt{1-Kx^{2}}}+x^{2}d\Omega^{2}\right]
\end{displaymath}](img6.png) |
(2.2) |
を代入する(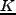 は曲率、
は曲率、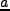 は scale factor を表わす)。ここで
は scale factor を表わす)。ここで 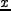 は共動座標
で、物理的な距離は
は共動座標
で、物理的な距離は 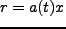 となる。以下、現在(
となる。以下、現在(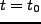 )の時に
)の時に
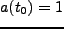 となるように正規化する。赤方偏移
となるように正規化する。赤方偏移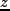 とは
とは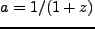 の関係で結
ばれる。さて、ここから独立な式として、
の関係で結
ばれる。さて、ここから独立な式として、
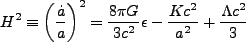 |
(2.3) |
及び
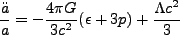 |
(2.4) |
を得る(Friedmann 方程式)。ここで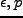 はそれぞれエネルギー密度と
圧力である。また、
はそれぞれエネルギー密度と
圧力である。また、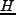 は Hubble parameter であり、屡々
は Hubble parameter であり、屡々
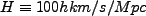 |
(2.5) |
と無次元量 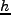 で表わす(最近の観測は
で表わす(最近の観測は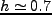 を示唆)。今回は
recombination 以降のみを扱うので、考えている物質はいわゆるダスト近似が可
能であり、
を示唆)。今回は
recombination 以降のみを扱うので、考えている物質はいわゆるダスト近似が可
能であり、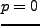 と置く(dark matter は圧力を感じない)。また密度
と置く(dark matter は圧力を感じない)。また密度
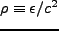 を定義しておく。
を定義しておく。
さて、平坦(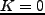 )で宇宙項なしの場合(Einstein-de Sitter宇宙)、
)で宇宙項なしの場合(Einstein-de Sitter宇宙)、
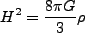 |
(2.6) |
となる。この時の密度を臨界密度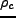 と定義すると、
と定義すると、
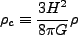 |
(2.7) |
となる。
ここで、参考までに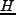 以外の宇宙論パラメータをまとめておく。
以外の宇宙論パラメータをまとめておく。
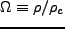 |
|
|
(2.8) |
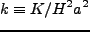 |
|
|
(2.9) |
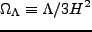 |
|
|
(2.10) |
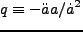 |
|
|
(2.11) |
と定義される。これらを用いると、Friedmann 方程式は
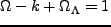 |
|
|
(2.12) |
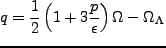 |
|
|
(2.13) |
となる。現在の値の宇宙論パラメータを用いると、一つめの式は
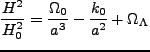 |
|
|
(2.14) |
となる(radiationが無視できる場合;
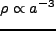 )。
)。
Subsections



Next: Friedmann方程式の意味
Up: note
Previous: はじめに
NAGASHIMA Masahiro
2009-03-12
![[*]](footnote.png)
![[*]](footnote.png)
![]() )で宇宙項なしの場合(Einstein-de Sitter宇宙)、
)で宇宙項なしの場合(Einstein-de Sitter宇宙)、
![]() 以外の宇宙論パラメータをまとめておく。
以外の宇宙論パラメータをまとめておく。