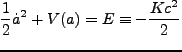Next: 輻射、物質、曲率、宇宙項が支配する時期
Up: 一様等方宇宙を記述する方程式
Previous: 一様等方宇宙を記述する方程式
ここで式(2.3)を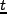 で微分し、出てきた
で微分し、出てきた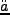 に式
(2.4)を代入すると、
に式
(2.4)を代入すると、
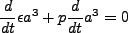 |
(2.15) |
が得られる。体積を 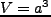 とし、内部エネルギーを
とし、内部エネルギーを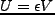 とすれば、
これは即ち
とすれば、
これは即ち
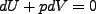 |
(2.16) |
となり、断熱膨張となっていることがわかる。実際には内部の物質の反応
により宇宙のエントロピーは増えているが、宇宙膨張自体は断熱変化である。
次に、式(2.3)を変形すると、
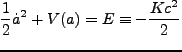 |
|
|
(2.17) |
 |
|
|
(2.18) |
となる(ここで
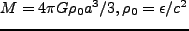 )。これは、
位置座標を
)。これは、
位置座標を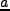 とした場合の、potential
とした場合の、potential 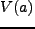 中での一次元の運動として解釈
できることを示している。FIG.1に、宇宙論パラメータを変
えた場合の定性的振舞いを示す。上の図において、現在の膨張率(
中での一次元の運動として解釈
できることを示している。FIG.1に、宇宙論パラメータを変
えた場合の定性的振舞いを示す。上の図において、現在の膨張率(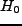 )は観
測より決まる量であるので、全てのモデルに対し fix されるが、宇宙年齢はパ
ラメータによって変化することがわかる。また特徴的な振舞いとして、宇宙項が
存在する場合は過去のある時期に potential の「頂上」付近を通るため(下図)
膨張が非常に遅くなる時期があり、宇宙年齢が伸びることになる。
)は観
測より決まる量であるので、全てのモデルに対し fix されるが、宇宙年齢はパ
ラメータによって変化することがわかる。また特徴的な振舞いとして、宇宙項が
存在する場合は過去のある時期に potential の「頂上」付近を通るため(下図)
膨張が非常に遅くなる時期があり、宇宙年齢が伸びることになる。
Figure 1:
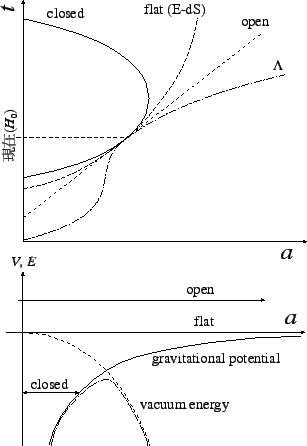 |
Figure 2:
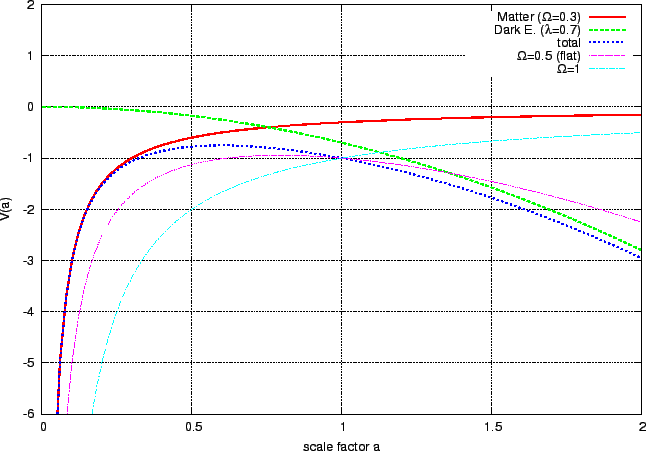 |
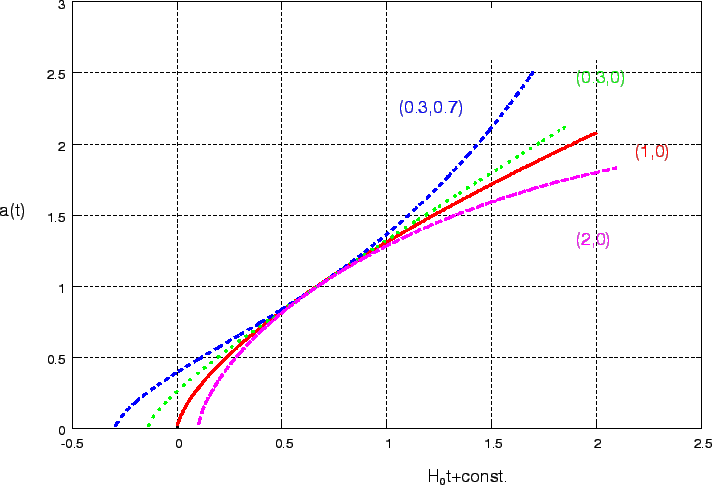
Figure 3:
 |
NAGASHIMA Masahiro
2009-03-12