


Next: 密度揺らぎの成長則
Up: 一様等方宇宙を記述する方程式
Previous: Friedmann方程式の意味
式(2.3)あるいは(2.14)の右辺の項のそれぞ
れが支配的になる時期を調べる(以下
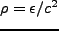 の質量密度で見る)。
エネルギー密度において、物質だけでなく輻射の寄与も考慮すると、各項の
scale factor に対する依存性は、輻射、物質、曲率、宇宙項の順に
の質量密度で見る)。
エネルギー密度において、物質だけでなく輻射の寄与も考慮すると、各項の
scale factor に対する依存性は、輻射、物質、曲率、宇宙項の順に
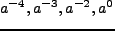 である。従って、これらの順に、宇宙膨張への
寄与が重要になる時期が現われる。宇宙初期には曲率や宇宙項は物質密度に比べ
て微小であり、宇宙膨張の振舞いは
である。従って、これらの順に、宇宙膨張への
寄与が重要になる時期が現われる。宇宙初期には曲率や宇宙項は物質密度に比べ
て微小であり、宇宙膨張の振舞いは
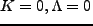 の Einstein-de Sitter 宇
宙とほぼ同じになる。
の Einstein-de Sitter 宇
宙とほぼ同じになる。
まず、輻射優勢期を見る。式(2.3)より、
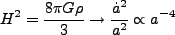 |
(2.19) |
であるから、
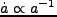 であり、
であり、
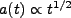 |
(2.20) |
となる。
やがて輻射のエネルギー密度は急速に落ち、物質の方が優勢になってくる。輻射
と物質のエネルギー密度が等しくなるのがほぼ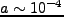 の頃である(導出
は省略。現在の宇宙背景輻射の温度と、温度が
の頃である(導出
は省略。現在の宇宙背景輻射の温度と、温度が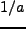 に比例することと、現在の物
質密度が与えられれば求められる)。物質が優勢の時期は、同様にして
に比例することと、現在の物
質密度が与えられれば求められる)。物質が優勢の時期は、同様にして
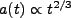 |
(2.21) |
となる。
やがて、曲率項が(あれば)効きだしてくる。この時期は、
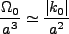 |
(2.22) |
となる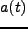 であるから、結局
であるから、結局
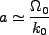 |
(2.23) |
であり、もし宇宙項が0(
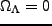 )とすると、
)とすると、
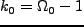 であるから
であるから
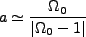 |
(2.24) |
となる。この場合、式(2.3)より
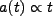 |
(2.25) |
となる。
もし宇宙項が存在し、宇宙が平坦(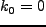 )であると、比較すべきは
)であると、比較すべきは
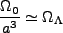 |
(2.26) |
となるので、宇宙項が支配的になるのは
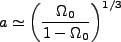 |
(2.27) |
となる。この場合は、
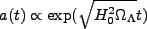 |
(2.28) |
と inflation 的膨張を起す。



Next: 密度揺らぎの成長則
Up: 一様等方宇宙を記述する方程式
Previous: Friedmann方程式の意味
NAGASHIMA Masahiro
2009-03-12
![]() の頃である(導出
は省略。現在の宇宙背景輻射の温度と、温度が
の頃である(導出
は省略。現在の宇宙背景輻射の温度と、温度が![]() に比例することと、現在の物
質密度が与えられれば求められる)。物質が優勢の時期は、同様にして
に比例することと、現在の物
質密度が与えられれば求められる)。物質が優勢の時期は、同様にして
![]() )であると、比較すべきは
)であると、比較すべきは