


Next: ピーク仮説
Up: より現実的な質量関数
Previous: モード間相関
次に、ハローはnon-zeroの領域でcollapseすることを考えてみよう。いままでは、
ハローは大きさを持っているにもかかわらず、空間上のある一点
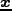 での
smoothing scale の異なる密度揺らぎの相関を考えてきた。しかし、実際には、
での
smoothing scale の異なる密度揺らぎの相関を考えてきた。しかし、実際には、
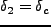 になる点の周囲で、
になる点の周囲で、
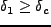 となる確率を、
smoothing scale の範囲内で平均したものを
となる確率を、
smoothing scale の範囲内で平均したものを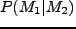 とする必要がある。
とする必要がある。
具体的には、
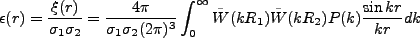 |
(4.167) |
と、二体相関関数を陽に考えることになる。
詳細は [10,17] に譲り、定性的傾向だけ解説する。宇宙全体では、
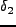 の平均は当然0である。従って、ある点で
の平均は当然0である。従って、ある点で
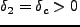 となっ
ていれば、その周囲では、確率的には
となっ
ていれば、その周囲では、確率的には
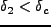 となっている方が多
いであろう。つまり、先程とは逆に、
となっている方が多
いであろう。つまり、先程とは逆に、
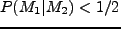 となっていると考えられ
る。従って、大質量ハローは増え、小質量ハローは減る、ということになる。
となっていると考えられ
る。従って、大質量ハローは増え、小質量ハローは減る、ということになる。
NAGASHIMA Masahiro
2009-03-12
![]() の平均は当然0である。従って、ある点で
の平均は当然0である。従って、ある点で
![]() となっ
ていれば、その周囲では、確率的には
となっ
ていれば、その周囲では、確率的には
![]() となっている方が多
いであろう。つまり、先程とは逆に、
となっている方が多
いであろう。つまり、先程とは逆に、
![]() となっていると考えられ
る。従って、大質量ハローは増え、小質量ハローは減る、ということになる。
となっていると考えられ
る。従って、大質量ハローは増え、小質量ハローは減る、ということになる。