


Next: ハローバイアス
Up: より現実的な質量関数
Previous: 空間相関
最後に、ハローは密度揺らぎの「ピーク」を中心にcollapseする、という仮説に
ついて考えてみよう[1,12]。
「ピーク」は空間分布に対するものなので、「ピーク」である条件としては、
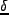 の空間微分が0:
の空間微分が0:
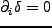
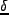 が上に凸、即ち二階微分の固有値がすべて負
が上に凸、即ち二階微分の固有値がすべて負
である。collapseするということから
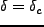 という条件も考慮する
と、成分としては0階微分が1個、1階微分が3個、2階微分が6個で計10個の成分を
考慮しなければならない。それに加えて
という条件も考慮する
と、成分としては0階微分が1個、1階微分が3個、2階微分が6個で計10個の成分を
考慮しなければならない。それに加えて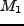 場で
場で
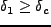 であ
る確率を求めるのであるから、11変数のGauss分布を解く必要がある。
であ
る確率を求めるのであるから、11変数のGauss分布を解く必要がある。
その振舞いはややこしいので結果については割愛するが、残された課題としては、
top-hat filter での peak formalism をどう構築するか、ということが挙げら
れよう。peak formalism では揺らぎの空間微分が重要な役割を果たすが、
top-hat filter は密度場を滑らかにしないため、微分(の分散)が発散する。
滑らかな filter を使い、最終的に limit を取って不連続な top-hat filter
にする、などの工夫が必要になろう。
Figure 12:
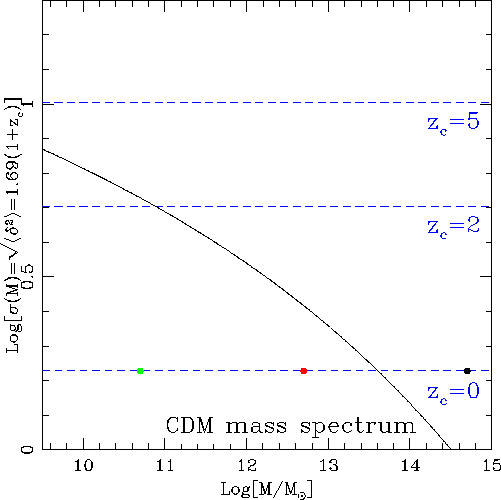 |
NAGASHIMA Masahiro
2009-03-12