

Next: 天体の個数密度
Up: 構造形成
Previous: 密度揺らぎの統計的性質
天体形成に至る非線型段階を記述するモデルとして、球対称に分布した揺らぎ
(質量M、半径r)に対する解がある。運動方程式は、単純に
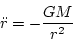 |
(32) |
であり、これがサイクロイド曲線を描くことは良く知られている。従って、揺ら
ぎの発展は、shell 内の平均密度が
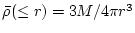 となるこ
とから求めることができる。rが再び0になる時点を collapse と定義すると、
E-dS宇宙の場合、線型成長を続けたとして
となるこ
とから求めることができる。rが再び0になる時点を collapse と定義すると、
E-dS宇宙の場合、線型成長を続けたとして
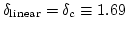 になった時が、実際の
になった時が、実際の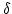 が発散する時刻に
相当することがわかる。従って、power spectrum の amplitude を、現在まで線
型成長を続けているとして normalize すると、ある点での揺らぎの大きさと、
その点が collapse する時刻
が発散する時刻に
相当することがわかる。従って、power spectrum の amplitude を、現在まで線
型成長を続けているとして normalize すると、ある点での揺らぎの大きさと、
その点が collapse する時刻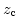 との間には、
との間には、
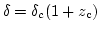 という関係のあることがわかる。
という関係のあることがわかる。
NAGASHIMA Masahiro
2000-10-23