
Next: 力学的テスト
Up: 構造形成
Previous: 球対称解
ここでは前節の球対称解と揺らぎの Gaussian 分布から、質量Mの天体の個数
密度
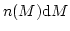 を見積る Press-Schechter 近似を紹介する[8]。まづ、
揺らぎを質量Mのスケール(
を見積る Press-Schechter 近似を紹介する[8]。まづ、
揺らぎを質量Mのスケール(
![$R\simeq[3M/4\pi\rho_0]^{1/3}$](img135.gif) )で均す。均され
た場で
)で均す。均され
た場で
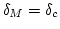 となった点が、質量Mの天体になると考える。
となった点が、質量Mの天体になると考える。
ここでWMは均すための window関数であり、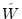 はそのFourier成分
である。window関数の形としては、top-hat 型や Gaussian型がよく用いられる
が、計算が簡単になるため Fourier空間での top-hat 型である sharp
k-space filter もよく用いられる。スケールMでの揺らぎの分散は、
はそのFourier成分
である。window関数の形としては、top-hat 型や Gaussian型がよく用いられる
が、計算が簡単になるため Fourier空間での top-hat 型である sharp
k-space filter もよく用いられる。スケールMでの揺らぎの分散は、
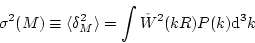 |
(35) |
となるが、window関数に入っている cut-off のスケールを
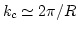 とすると、
とすると、
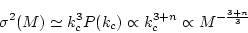 |
(36) |
となる。ここで、
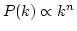 とおいた。5.2で述べ
たように、CDMモデルでは
とおいた。5.2で述べ
たように、CDMモデルでは
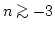 となる。
となる。
さて、Mの場でcollapse している領域は
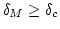 であるので、
その割合は
であるので、
その割合は
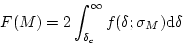 |
(37) |
と書ける。ここで factor 2 は、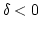 の領域も含めて全領域を考慮するた
めにつけられている。この領域が質量M以上の天体に含まれているので、
の領域も含めて全領域を考慮するた
めにつけられている。この領域が質量M以上の天体に含まれているので、
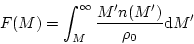 |
(38) |
と関係づけられる。質量Mの天体の個数密度は、M以上の天体になっている領
域から
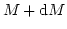 以上の天体になっている領域を引いたものを、一つのMの天体が
占める領域
以上の天体になっている領域を引いたものを、一つのMの天体が
占める領域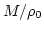 で割ったものに等しいから、
で割ったものに等しいから、
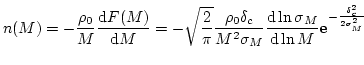 |
|
|
(39) |
となる。これをPress-Schechter質量関数と呼ぶが、n>-3の場合のみ適用可能
であることに注意しなければならない。
NAGASHIMA Masahiro
2000-10-23
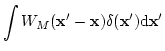
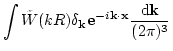
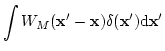
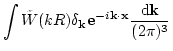
![]() であるので、
その割合は
であるので、
その割合は