

Next: 銀河団の質量-光度比
Up: 力学的テスト
Previous: 力学的テスト
SDSS計画のような銀河サーベイは、奥行き方向の分布については赤方偏移が座標
となっている。観測される赤方偏移には Hubble flow のみでなく、個々の銀河
の固有速度が含まれる。固有速度は速度揺らぎであるので、5.1
で述べたように、その大きさは宇宙論パラメータに依存する。一方、視線に垂直
な方向の分布には無関係であるので、power spectrum の方向依存性を測れば、
宇宙論パラメータを決めることができる。
ここで、実空間座標を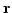 、赤方偏移空間での座標を
、赤方偏移空間での座標を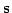 と置く。固有速度の
視線方向成分は、視線方向の単位ベクトルを
と置く。固有速度の
視線方向成分は、視線方向の単位ベクトルを
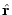 として
として
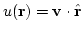 と書ける。以下、簡単のためH=1となる単位系を用い
る。実空間と赤方偏移空間の関係は、
と書ける。以下、簡単のためH=1となる単位系を用い
る。実空間と赤方偏移空間の関係は、
![\begin{displaymath}{\bf s}={\bf r}\left[1+\frac{u({\bf r})-u({\bf0})}{r}\right]
\end{displaymath}](img156.gif) |
(40) |
で表される。実空間での密度
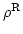 と赤方偏移空間での密度
と赤方偏移空間での密度
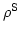 の関係は、質量保存
の関係は、質量保存
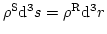 より、
より、
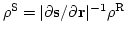 と表される。この
Jacobian を求めると、
と表される。この
Jacobian を求めると、
![\begin{displaymath}{\rm d}^3s=\left[1+\frac{u({\bf r})-u({\bf0})}{r}\right]^2\left[1+\frac{{\rm d}u({\bf r})}{{\rm d}r}\right]{\rm d}^3 r
\end{displaymath}](img161.gif) |
(41) |
となり、
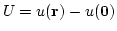 とおくと、密度は
とおくと、密度は
![\begin{displaymath}\rho^{\rm S}=\left[1-2\frac{U}{r}-\frac{{\rm d}U}{{\rm d}r}\right]\rho^{\rm R}
\end{displaymath}](img163.gif) |
(42) |
となる。ここで、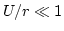 であるので、一次までを取った。さらに、十分遠方
の観測者に対しては、
であるので、一次までを取った。さらに、十分遠方
の観測者に対しては、
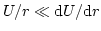 となることを用いると、密度コントラ
ストは
となることを用いると、密度コントラ
ストは
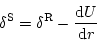 |
(43) |
と書ける。
次に線型理論を用いると、連続の式(18)より、
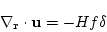 |
(44) |
を得る。さらにPoisson方程式(20)を用いると、
![\begin{displaymath}{\bf u}=-Hf\frac{\nabla_{{\bf r}}\phi}{4\pi G\rho_0}=-Hf\nabla_{{\bf r}}[\Delta^{-1}\delta]
\end{displaymath}](img168.gif) |
(45) |
となる。ここで注意すべきことは、上式の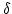 は重力を規定する質量(CDM)分布を
表しているが、観測されるのは銀河分布
は重力を規定する質量(CDM)分布を
表しているが、観測されるのは銀河分布
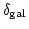 であることである。
これらをつなぐ最も簡単な関係式として、
であることである。
これらをつなぐ最も簡単な関係式として、
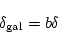 |
(46) |
が仮定される。ここでbは bias parameter と呼ばれる。ここで
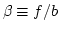 と定義すると、速度揺らぎは
と定義すると、速度揺らぎは
![\begin{displaymath}{\bf u}=-H\beta\nabla_{{\bf r}}\left[\Delta^{-1}\delta_{\rm gal}\right]
\end{displaymath}](img172.gif) |
(47) |
となる。ここで
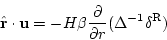 |
(48) |
であるから、
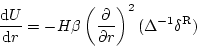 |
(49) |
となり、これを代入すると
![\begin{displaymath}\delta^{\rm S}=\left[1+\beta\left(\frac{\partial}{\partial r}\right)^2\Delta^{-1}\right]\delta^{\rm R}
\end{displaymath}](img175.gif) |
(50) |
という関係が得られる。さらにこれをFourier変換すると、
![\begin{displaymath}\delta_{{\bf k}}^{\rm S}=[1+\beta\mu_{{\bf k}}^2]\delta_{{\bf k}}^{\rm R}
\end{displaymath}](img176.gif) |
(51) |
(ここで
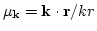 )となることから、赤方偏移空間でのpower
spectrum は
)となることから、赤方偏移空間でのpower
spectrum は
![\begin{displaymath}P^{\rm S}({\bf k})=[1+\beta\mu_{{\bf k}}^2]^2P^{\rm R}(k)
\end{displaymath}](img178.gif) |
(52) |
となる。
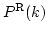 は等方なので、
は等方なので、
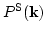 の角度依存性を調べれ
ば、
の角度依存性を調べれ
ば、
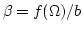 が求まる。最近では、弱非線型理論や観測者が近い場
合などへも拡張されている。またmultipole展開をすることで、より見やすい形
に書くこともなされている。
が求まる。最近では、弱非線型理論や観測者が近い場
合などへも拡張されている。またmultipole展開をすることで、より見やすい形
に書くこともなされている。


Next: 銀河団の質量-光度比
Up: 力学的テスト
Previous: 力学的テスト
NAGASHIMA Masahiro
2000-10-23
![]() 、赤方偏移空間での座標を
、赤方偏移空間での座標を![]() と置く。固有速度の
視線方向成分は、視線方向の単位ベクトルを
と置く。固有速度の
視線方向成分は、視線方向の単位ベクトルを
![]() として
として
![]() と書ける。以下、簡単のためH=1となる単位系を用い
る。実空間と赤方偏移空間の関係は、
と書ける。以下、簡単のためH=1となる単位系を用い
る。実空間と赤方偏移空間の関係は、
![\begin{displaymath}\delta^{\rm S}=\left[1+\beta\left(\frac{\partial}{\partial r}\right)^2\Delta^{-1}\right]\delta^{\rm R}
\end{displaymath}](img175.gif)