

Next: まとめと展望
Up: 力学的テスト
Previous: Redshift distortion
銀河団中のbaryon質量は、optical の観測から得られる銀河の個数と、X線光度
から得られる銀河団ガス(ICM)から求めることができる。一方、全質量
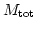 は、銀河同士の速度分散を測れば得られる。全銀河の質量を
は、銀河同士の速度分散を測れば得られる。全銀河の質量を
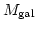 、
ICMの質量を
、
ICMの質量を
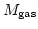 とすると、銀河団からbaryonが逃げないとすれば、
とすると、銀河団からbaryonが逃げないとすれば、
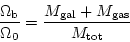 |
(53) |
となり、Big Bang 元素合成理論から
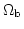 を与えてやれば
を与えてやれば
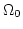 が求まる。ここで
が求まる。ここで
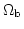 は baryon 密度パラメータである。
は baryon 密度パラメータである。
以下の議論は White et al. (1993)の議論に基づく[10]。Coma銀河団の観
測より、全銀河の光度が
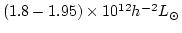 と求まっ
ている(
と求まっ
ている(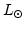 は太陽光度)。一方、幾つかの銀河の観測から、銀河の質量-
光度比が
[M/L]=8.0h(L/L*)0.35であることがわかっている([]は太陽の質
量-光度比を単位としていることを示す。また
は太陽光度)。一方、幾つかの銀河の観測から、銀河の質量-
光度比が
[M/L]=8.0h(L/L*)0.35であることがわかっている([]は太陽の質
量-光度比を単位としていることを示す。また
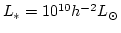 )。
Coma銀河団銀河の光度関数を用いて平均すると、
)。
Coma銀河団銀河の光度関数を用いて平均すると、
![$\langle[M/L]\rangle=6.4h$](img190.gif) と
なる。ここから、銀河の総質量を求めると、
と
なる。ここから、銀河の総質量を求めると、
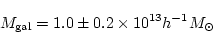 |
(54) |
となる。一方、X線の観測から、ICMの質量が
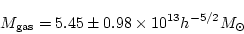 |
(55) |
と求まっている。
DMを含む全質量の評価には様々な方法があるが、静水圧平衡
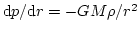 (圧力pはガスなら
(圧力pはガスなら
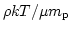 、銀河分布なら
、銀河分布なら
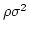 とすればよい)からは大体
とすればよい)からは大体
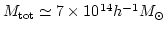 と求まっている。また数値シミュレーションからは、
およそ
と求まっている。また数値シミュレーションからは、
およそ
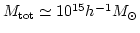 という値が得られている。
という値が得られている。
以上の値から、
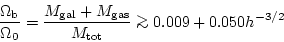 |
(56) |
という結果が得られている。元素合成理論から予想される、
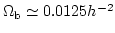 という値を用いると、およそ
という値を用いると、およそ
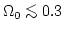 という
制限が得られることになる。
という
制限が得られることになる。
NAGASHIMA Masahiro
2000-10-23
![]() と求まっ
ている(
と求まっ
ている(![]() は太陽光度)。一方、幾つかの銀河の観測から、銀河の質量-
光度比が
[M/L]=8.0h(L/L*)0.35であることがわかっている([]は太陽の質
量-光度比を単位としていることを示す。また
は太陽光度)。一方、幾つかの銀河の観測から、銀河の質量-
光度比が
[M/L]=8.0h(L/L*)0.35であることがわかっている([]は太陽の質
量-光度比を単位としていることを示す。また
![]() )。
Coma銀河団銀河の光度関数を用いて平均すると、
)。
Coma銀河団銀河の光度関数を用いて平均すると、
![]() と
なる。ここから、銀河の総質量を求めると、
と
なる。ここから、銀河の総質量を求めると、
![]() (圧力pはガスなら
(圧力pはガスなら
![]() 、銀河分布なら
、銀河分布なら
![]() とすればよい)からは大体
とすればよい)からは大体
![]() と求まっている。また数値シミュレーションからは、
およそ
と求まっている。また数値シミュレーションからは、
およそ
![]() という値が得られている。
という値が得られている。