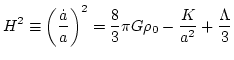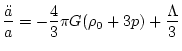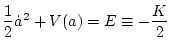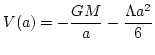

Next: Hubble parameter H
Up: 宇宙論的構造形成と観測的宇宙論
Previous: はじめに
まづ、宇宙モデルを記述する基本方程式、Friedmann 方程式の定性的振舞いを調
べることにする。一様・等方性から導かれる Robertson-Walker metric を用い
ると、
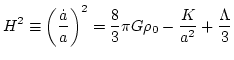 |
|
|
(1) |
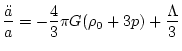 |
|
|
(2) |
となる。ここで、aは scale factor、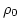 は宇宙の平均密度、pは
圧力、Kは曲率、
は宇宙の平均密度、pは
圧力、Kは曲率、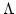 は宇宙定数である。H以外の宇宙論パラメータは、
これらを用いて、
は宇宙定数である。H以外の宇宙論パラメータは、
これらを用いて、
と定義される。ここで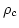 は critical density であり、
は critical density であり、
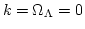 、即ち Einstein-de Sitter 宇宙における宇宙の平均密
度である。
ここで、式(1)を変形すると、
、即ち Einstein-de Sitter 宇宙における宇宙の平均密
度である。
ここで、式(1)を変形すると、
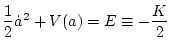 |
|
|
(7) |
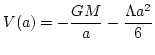 |
|
|
(8) |
となる(ここで
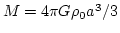 )。これは、位置座標をaとした場
合の、potential V(a) 中での一次元の運動として解釈できることを示してい
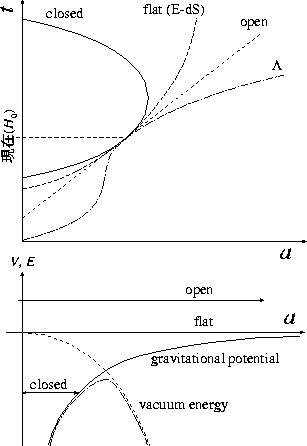
る。FIG.1に、宇宙論パラメータを変えた場合の定性的振舞
いを示す。上の図において、現在の膨張率(H0)は観測より決まる量である
ので、全てのモデルに対し fix されるが、宇宙年齢はパラメータによって変化
することがわかる。また特徴的な振舞いとして、宇宙項が存在する場合は過去の
ある時期に potential の「頂上」付近を通るため(下図) 膨張が非常に遅くなる
時期があり、宇宙年齢が伸びることになる。
)。これは、位置座標をaとした場
合の、potential V(a) 中での一次元の運動として解釈できることを示してい
る。FIG.1に、宇宙論パラメータを変えた場合の定性的振舞
いを示す。上の図において、現在の膨張率(H0)は観測より決まる量である
ので、全てのモデルに対し fix されるが、宇宙年齢はパラメータによって変化
することがわかる。また特徴的な振舞いとして、宇宙項が存在する場合は過去の
ある時期に potential の「頂上」付近を通るため(下図) 膨張が非常に遅くなる
時期があり、宇宙年齢が伸びることになる。
Figure 1:
 |
NAGASHIMA Masahiro
2000-10-23